본 게시글은 대학 전공수업을 들으며 노션에 정리한 내용을 블로그로 옮긴 것으로, 노션 웹을 통해 최적화된 형태로 읽으시길 권장드립니다.(➡️ 노션 링크)
기본 사항
디지털 논리회로

- 디지털 컴퓨터의 수학적 구조는 이진법이다.
- 이진법: 0과 1 두개의 숫자만을 이용해 모든 수를 표현! 즉, 0 or 1 !
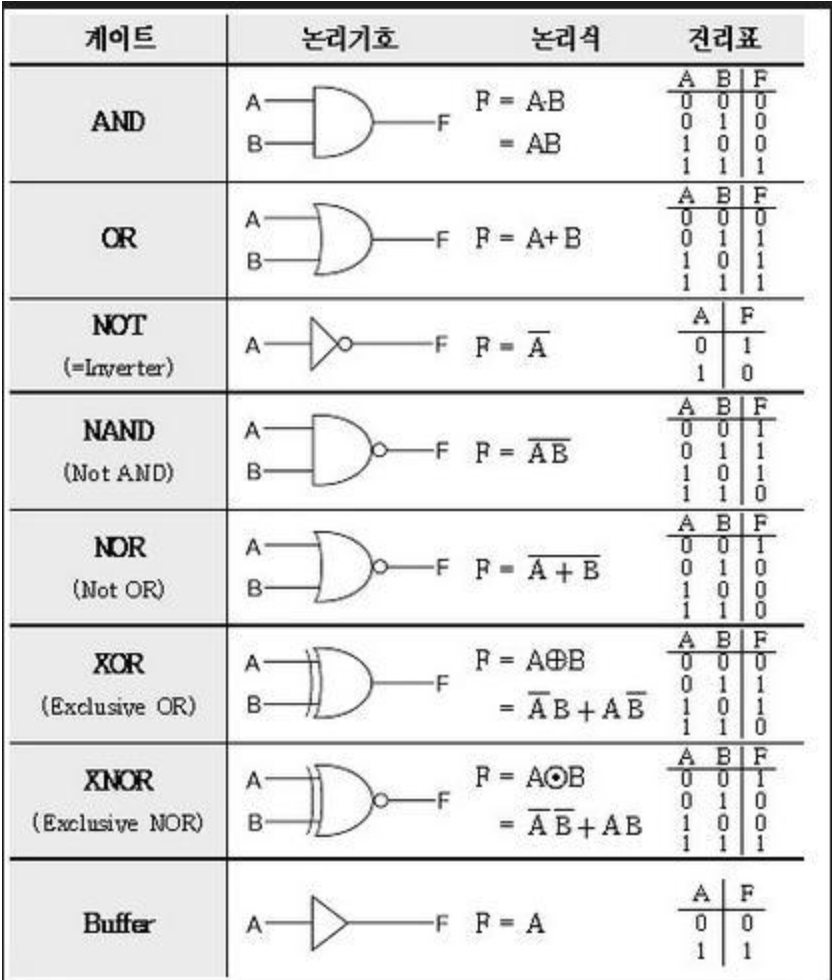
기본 논리게이트(logical gate)
*image source: https://www.researchgate.net/figure/Summary-of-the-common-Boolean-logic-gates-with-symbols-and-truth-tables_fig3_291418819
참고:
기본 논리게이트의 식과 모양을 확실히 익힐 것!
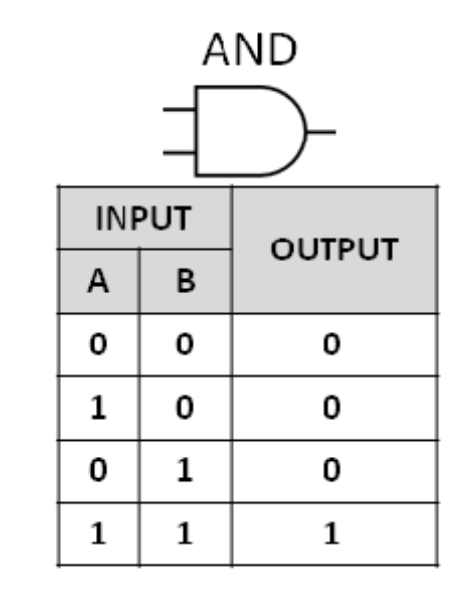
AND
F = X﹒Y
논리곱(𝒑∧𝒒)
두 입력 모두 1일 때만 1 출력
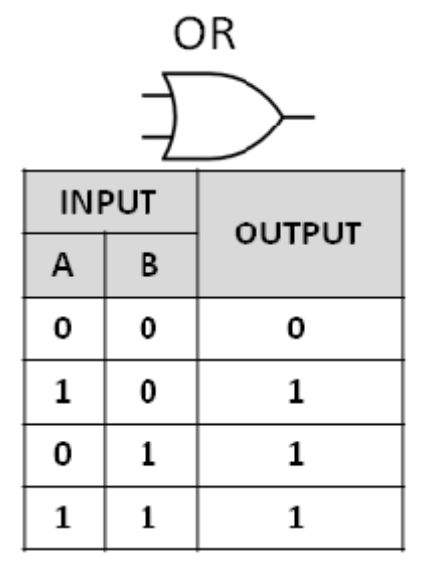
OR
F = X + Y
논리합 (𝒑∨𝒒)
두 입력 중 하나라도 1이면 1 출력
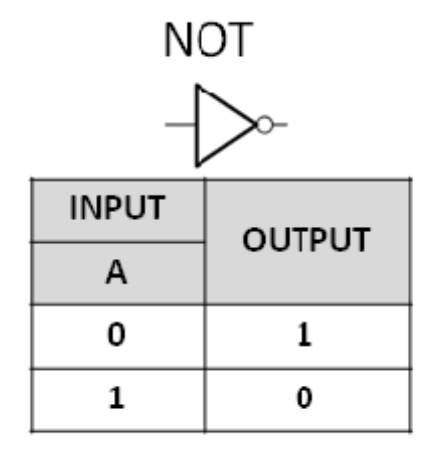
NOT
F = $\overline{X}$
논리부정 (~𝒑)
입력 1이면 0 출력, 입력 0이면 1 출력
기타 논리게이트
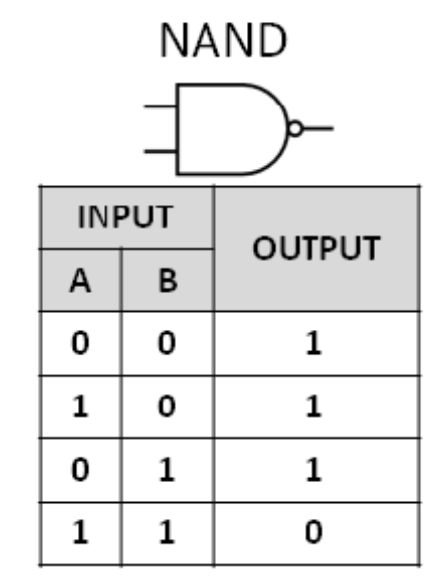
NAND
F = $\overline{X﹒Y} = \overline{X} + \overline{Y}$
(by 드모르간 법칙)
AND 게이트 출력을 NOT.
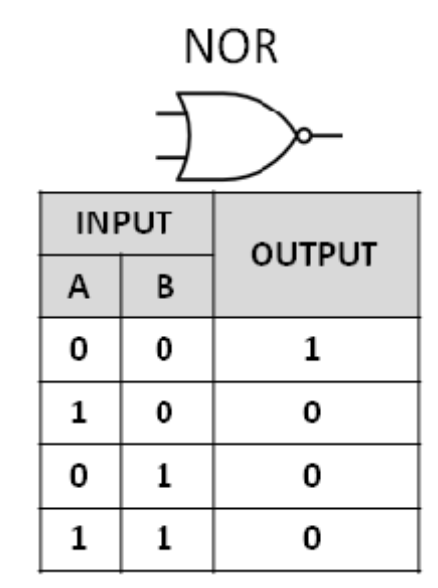
NOR
F = $\overline{X+Y} = \overline{X}﹒\overline{Y}$
(by 드모르간 법칙)
OR 게이트 출력을 NOT
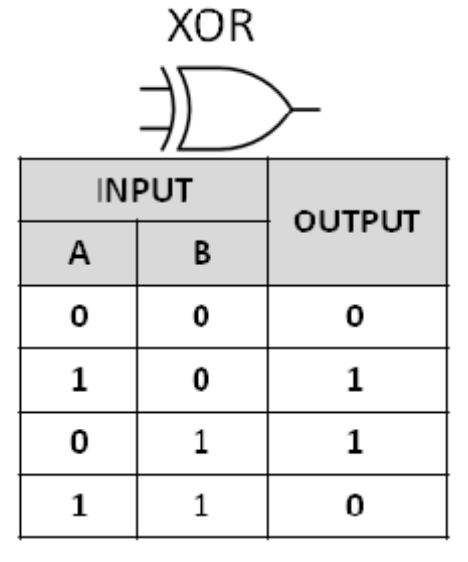
XOR(배타곱)
$F = 𝑿⨁𝒀\=\overline{X}Y + X\overline{Y}$
두 입력이 서로 다를 때만 1 출력
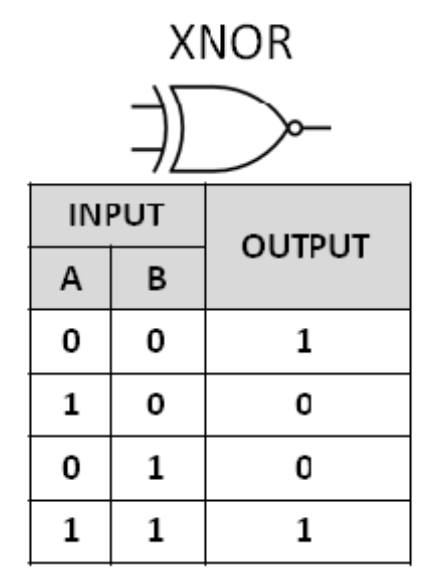
XNOR
$F = \overline{𝑿⨁𝒀}\=\overline{\overline{X}Y+X\overline{Y}} \=\overline{X}\space \overline{Y}+XY$
두 입력이 서로 같으면 1 출력
부울대수(Boolean Algebra)
소개
이진 변수(T/F , 1/0)를 사용하여 논리 연산을 수행하는 연산 체계
부울 변수
두 가지 값(참 또는 거짓, 1 또는 0) 중 하나를 가질 수 있는 변수(A,B,C…)
부울 상수
:1(True), 0(False)
부울연산자
∙ (AND) : A⋅B 또는 𝐴∧𝐵
- (OR) : A+B 또는 𝐴∨𝐵
- $\overline{A}$ (NOT) : ~A
부울식
부울식은 순환적으로 정의한다.
- 부울상수 0, 1은 부울식이다.
- 부울변수는 부울식이다.
- 𝑿, 𝒀가 부울식일 때, 𝑿 + 𝒀, 𝑿 ∙ 𝒀, $\overline{X}$, (𝑿) 도 부울식이다.
성질
부울대수의 기본 정리
https://homubee.tistory.com/31
논리와 부울대수의 관련성
- 𝒑, 𝒒, 𝒓 ⟺ 𝑿, 𝒀, 𝒁
- 𝑻 ⟺ 𝟏
- 𝑭 ⟺ 𝟎
- AND (∧) ⟺ ∙
- OR (∨) ⟺ +
- NOT (~) ⟺ ᅳ
- 항등법칙
- 지배법칙
- 멱등법칙
- 부정법칙
- 교환법칙
- 결합법칙
- 분배법칙
쌍대성 원리(principle of duality)
부울식에서 +와 ∙를 맞바꾸고, 논리값 0과 1을 맞바꿀 때 원래 부울식의 쌍대(dual)을 얻게됨.
ex)
𝑿 + 𝟎 = 𝑿 과 𝑿 ∙ 𝟏 = 𝑿는 쌍대형태
𝑿 + 𝟏 = 𝟏 와 𝑿 ∙ 𝟎 = 𝟎는 상대형태
드모르간 법칙의 일반화
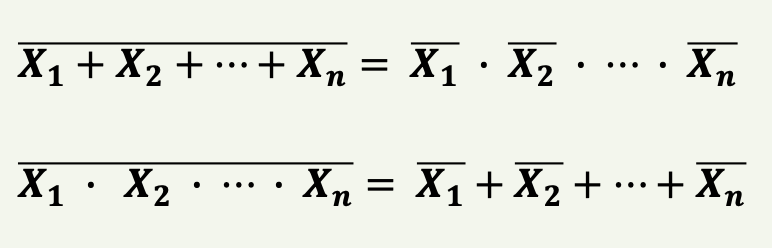
부울함수의 보수
부울함수 𝑭의 보수는 $\overline{F}$
구하는 방법 :
(1) 드 모르간 법칙 이용
(2) 쌍대성 원리 이용
- 𝑭의 쌍대 구함
- 𝑭의 쌍대에서 정상형(𝑿)과 보수형($\overline{X}$)을 서로 바꿈
부울함수의 대수적 간소화(algebraic simplification)
주어진 부울함수에 대하여 부울대수의 정리를 이용하여 변환한 다음, 변환된 여러 함수 중 가장 간단한 형태의 함수를 찾아내는 것.
간소화 목적(why?)
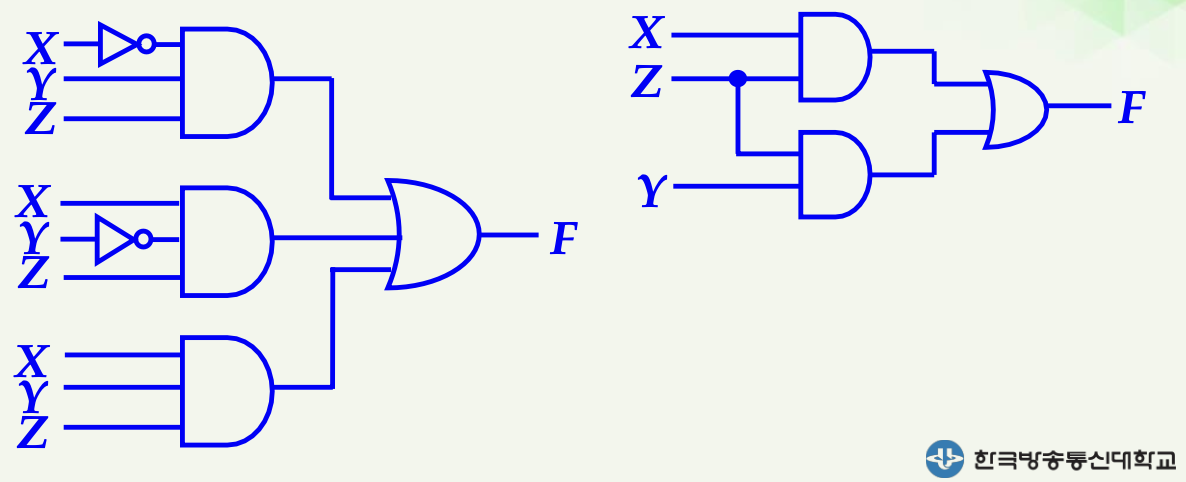
왼쪽과 오른쪽 회로의 결과값이 똑같을 때, 단순한 오른쪽이 탁월하다!
복잡한 부울함수는 복잡한 논리회로를, 간단한 부울함수는 간단한 논리회로를 갖는다.
즉, 논리회로를 구성하는 게이트의 수와 게이트의 입력을 나타내는 변수의 수를 줄여 논리회로를 간소화 하는 것이 목적!
간소화 예
항 결합

문자소거

중복항 첨가

'Computer Science > 이산수학' 카테고리의 다른 글
| [이산수학] 그래프 : 용어(동형,방향,무향...), 탐색(워크,트레일,경로), 종류(완전,이분,정규), 표현(발생/인접행렬, 인접리스트), 오일러투어, 4색정리, 해밀턴경로 (0) | 2024.06.22 |
|---|---|
| [이산수학] 관계 : 표현법, 성질(반사,대칭,추이), 종류(역,합성,동치) (0) | 2024.06.22 |
| [이산수학] 행렬 : 연산(합,차,곱), 가우스 소거법, 행렬 종류(행제형,정방,대각,단위,대칭,삼각,전치,역,부울행렬) (0) | 2024.06.22 |
| [이산수학] 집합론 : 표시법, (진)부분집합, 서로소, 분할, 멱집합, 연산(합,교,차,여,곱), 대수법칙 (0) | 2024.06.22 |
| [이산수학] 증명 : 용어(공리, 정리) 직접 증명법, 귀납법, 간접 증명법(대우,모순,존재,전수) (2) | 2024.06.22 |
| [이산수학] 논리와 명제 : 논리기호, 합성명제, (쌍)조건 명제, 한정자, 추론 (0) | 2024.06.22 |
