본 게시글은 대학 전공수업을 들으며 노션에 정리한 내용을 블로그로 옮긴 것으로, 노션 웹을 통해 최적화된 형태로 읽으시길 권장드립니다.특히 행렬 표현은 제대로 되지 않는 문제가 있습니다.(티스토리의 HTML 변환시 문제가 발생하는 것 같습니다.)(➡️ 노션 링크)
6강 - 관계
관계
미리 알아둘 사항
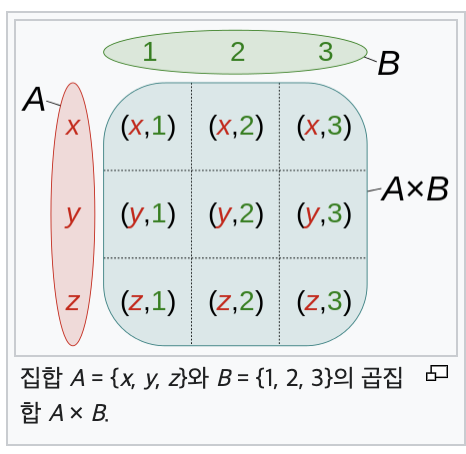
집합X에서 집합Y 로의 이항관계(binary relation) R은 𝑿 × 𝒀의 부분집합!
- (𝒙, 𝒚) ∈ 𝑹⇒ 𝒙𝑹𝒚로 표기
- ⇒ 𝒙는 𝒚와 𝑹의 관계가 있다.
- 𝑿 = 𝒀 이면 ⇒ 𝑹을 𝑿에서의 관계
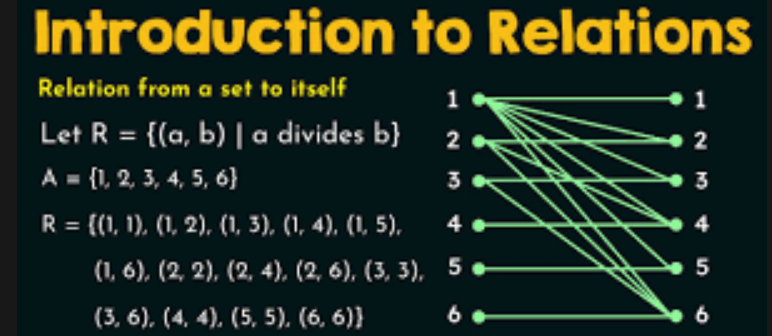
- https://math24.net/binary-relations.html
- 예시
관계의 표현
화살표 도표
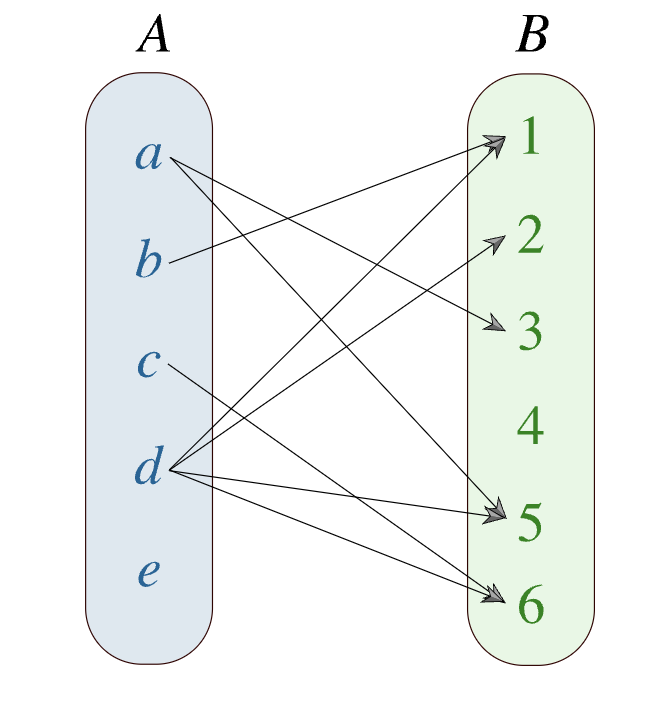
집합 A = {a,b,c,d,e}, 집합 B = {1,2,3,4,5,6} 이고
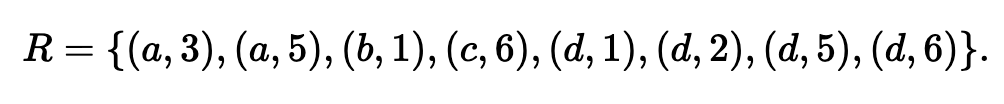
일때, 이를 화살표 도표로 나타내면
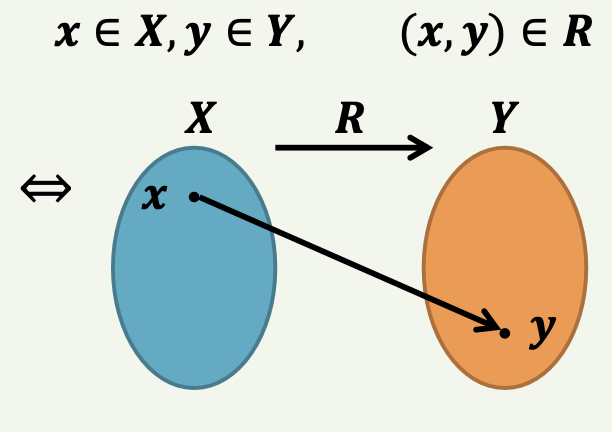
방향 그래프
그래프 *:** 점[꼭지점](vertex)과 선[변](edge)으로 이루어진 도형
- G = (V, E)
$$
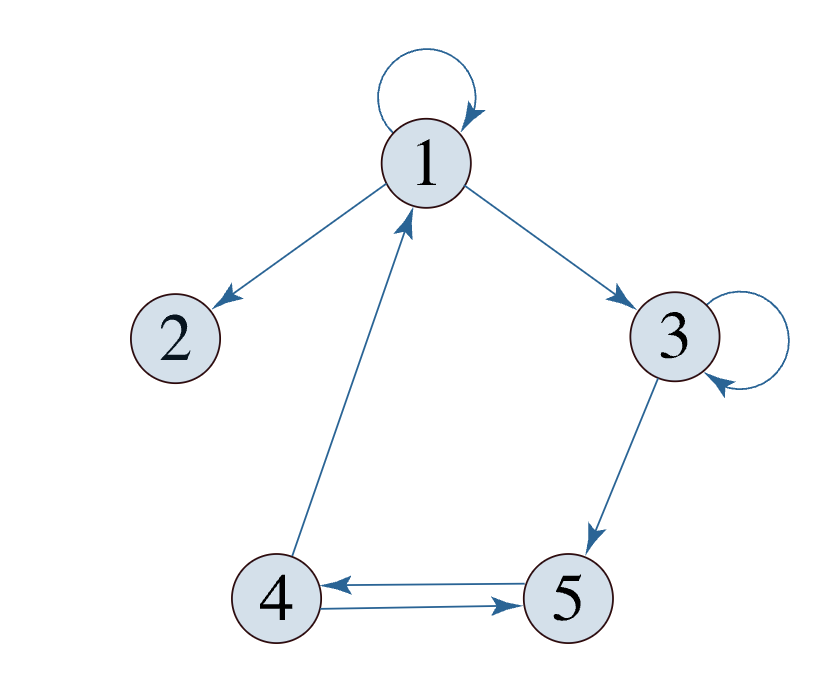
A = {1, 2, 3, 4, 5} 이고, \
R = {(1,1), (1,2), (1,3), (3,3), (3,5), (4,1), (4,5), (5,4)}
$$
일 때의 방향그래프 :
https://math24.net/binary-relations.html
부울행렬
𝑨 = 𝟏, 𝟐, 𝟑
𝑻 = { (𝟏, 𝟏) , (𝟏, 𝟐) , (𝟐, 𝟏) , (𝟐, 𝟐) , (𝟑, 𝟏) , (𝟑, 𝟐) }
관계 T를 부울행렬로 나타내면
$M_T =\begin{pmatrix}
1 & 1 & 0 \
1 & 1 & 0 \
1 & 1 & 0 \
\end{pmatrix}
이고, \space |T| = 6$
관계의 성질
성질의 종류
반사적 (reflexive)
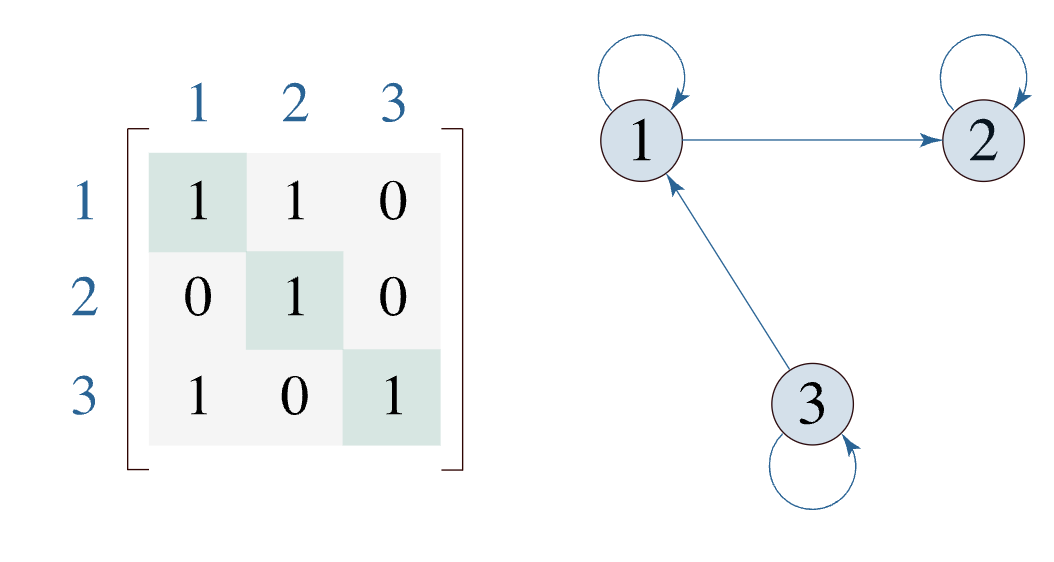
집합 A에서의 관계 R에 대해 ∀𝒂 ∈ 𝑨이면, (𝒂, 𝒂) ∈ 𝑹
즉, 모든 𝒂 ∈ 𝑨에 대해 (𝒂, 𝒂) ∈ 𝑹이면, R은 반사적이다.
https://math24.net/properties-relations.html
방향 그래프를 그렸을 때 자기 자신으로 돌아오는 게 모두 있는 것
대칭적 (symmetric)
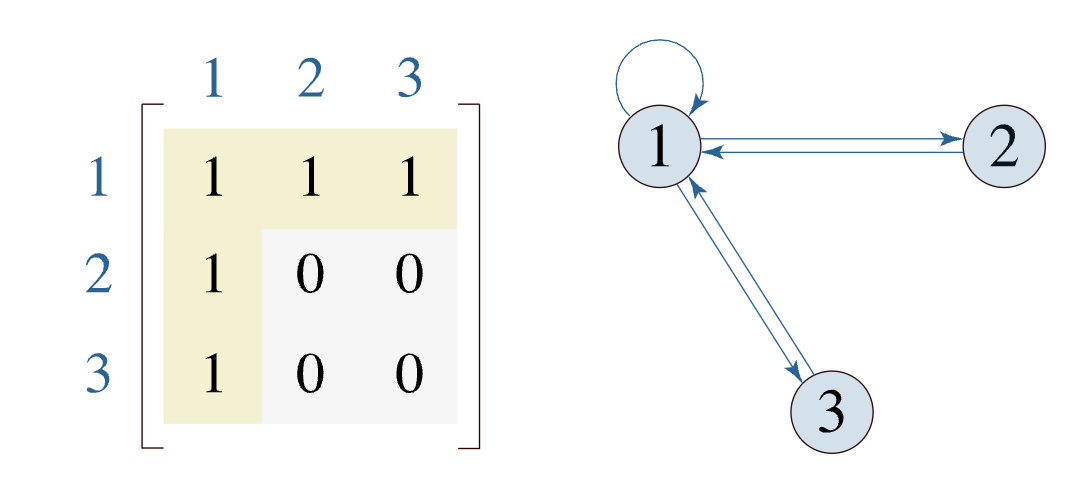
∀𝒂, 𝒃 ∈ 𝑨, (𝒂, 𝒃) ∈ 𝑹 ⇒ (𝒃, 𝒂) ∈ 𝑹
모든 𝒂, 𝒃 ∈ 𝑨에 대해, (𝒂, 𝒃) ∈ 𝑹일 때 (𝒃, 𝒂) ∈ 𝑹이면 대칭적이다.
https://math24.net/properties-relations.html
가는게 있으면 오는게 있는 것
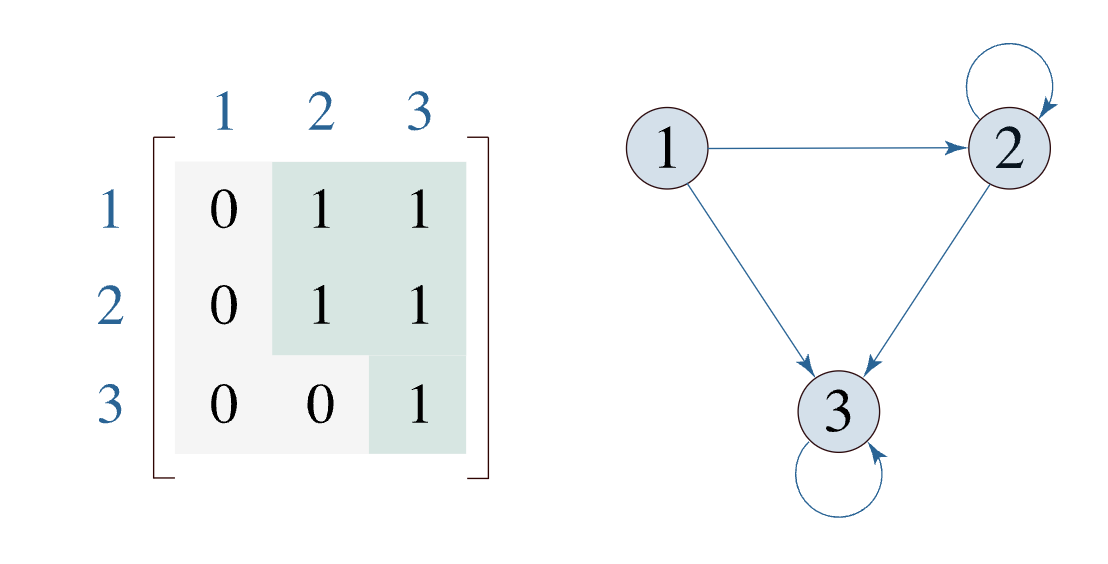
추이적 (transitive)
∀𝒂, 𝒃, 𝒄 ∈ 𝑨, ((𝒂, 𝒃) ∈ 𝑹 $\land$ (𝒃, 𝒄) ∈ 𝑹) ⇒ (𝒂, 𝒄) ∈ 𝑹
즉, 모든 𝒂, 𝒃, 𝒄 ∈ 𝑨에 대해, (𝒂, 𝒃) ∈ 𝑹이고 (𝒃, 𝒄) ∈ 𝑹일 때,
(𝒂, 𝒄) ∈ 𝑹이면 𝑹은 추이적이다.
https://math24.net/properties-relations.html
두번 돌아 가는 길이 있으면, 직접 가는 길도 있어야한다.
(노드 𝑎에서 𝑏로 가는 경로와 𝑏에서 𝑐로 가는 경로가 있다면,
𝑎에서 𝑐로 가는 경로도 존재한다.)
성질과 부울행렬
반사적
∀𝒂 ∈ 𝑨, (𝒂, 𝒂) ∈ 𝑹
$M_R = \begin{pmatrix}
1 & \cdots & \cdots \
\cdots & 1 & \cdots \
\cdots & \cdots & 1 \
\end{pmatrix}$
대칭적
∀𝒂, 𝒃 ∈ 𝑨, 𝒂, 𝒃 ∈ 𝑹 ⇒ (𝒃, 𝒂) ∈ 𝑹
$M_R = \begin{pmatrix}
1 & 1 & \cdots \
1 & 1 & \cdots \
\cdots & \cdots & 1 \
\end{pmatrix}$
추이적
∀𝒂, 𝒃, 𝒄 ∈ 𝑨, ((𝒂, 𝒃) ∈ 𝑹 ٿ (𝒃, 𝒄) ∈ 𝑹) ⇒ (𝒂, 𝒄) ∈ 𝑹
$M_R = \begin{pmatrix}
1 & 1 & 1 \
\cdots & 1 & 1 \
\cdots & \cdots & 1 \
\end{pmatrix}$
관계의 종류
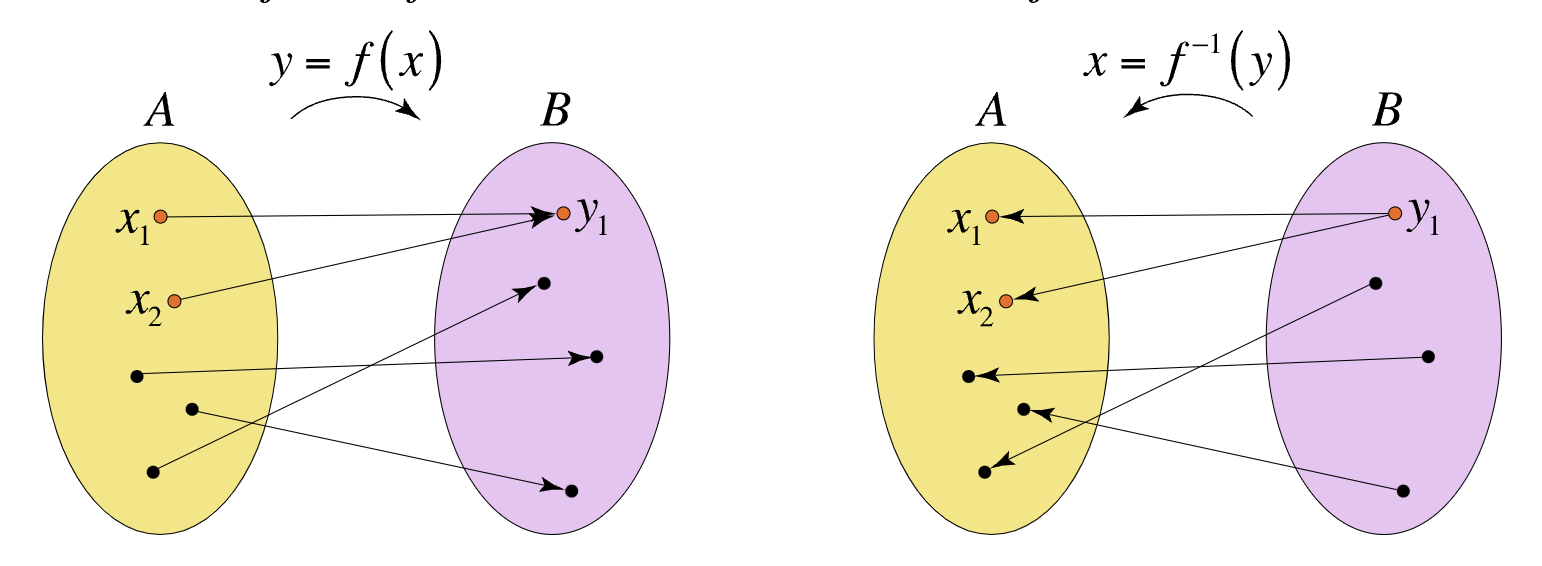
역관계(Inverse Relation)
관계 𝑅이 𝐴에서 𝐵로의 관계라면, 역관계 𝑅−1는 𝐵에서 𝐴로의 관계.
𝑹−𝟏 = {(𝒚, 𝒙) | (𝒙, 𝒚) ∈ 𝑹 } ⊂ 𝒀 × 𝑿
https://math24.net/inverse-functions.html
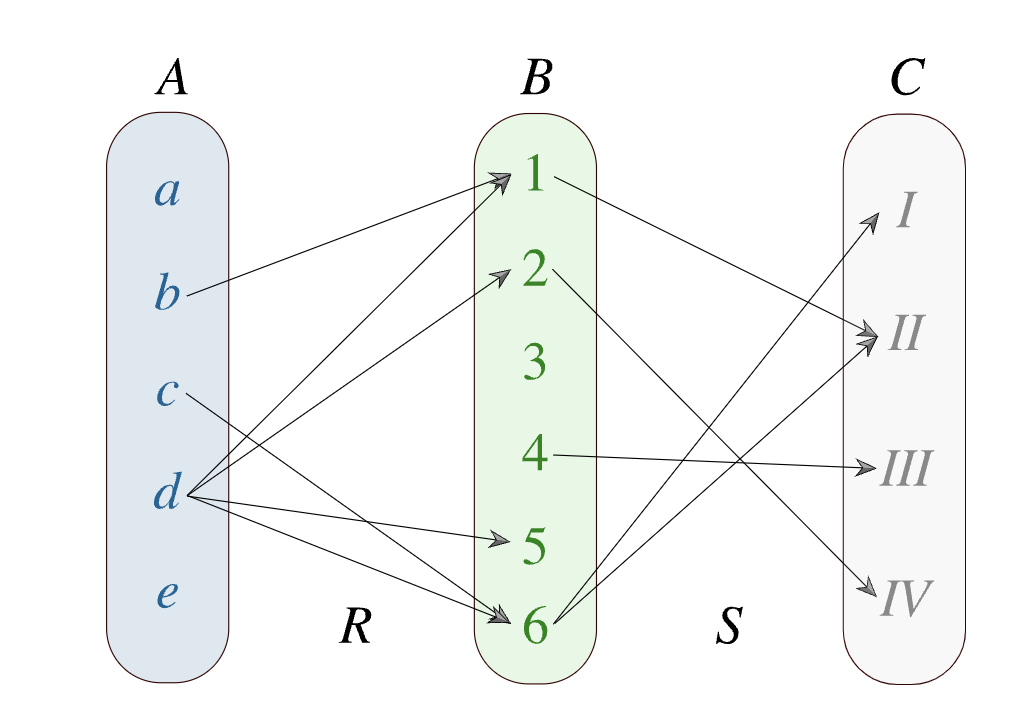
합성관계(composition relation)
집합 𝑨, 𝑩, 𝑪, 𝑹을 𝑨에서 𝑩로의 관계, 𝑺를 𝑩에서 𝑪로의 관계라고 할 때
𝑹과 𝐒의 합성관계(composition relation)
𝑺 ∘ 𝑹 = {(𝒂, 𝒄) | 𝒂 ∈ 𝑨, 𝒃 ∈ 𝑩, 𝒄 ∈ 𝑪, (𝒂, 𝒃) ∈ 𝑹, (𝒃, 𝒄) ∈ 𝑺 }
𝑺 ∘ 𝑹 ⊂ 𝑨 × 𝑪 (𝑨에서 𝑪로의 관계)
https://math24.net/composition-relations
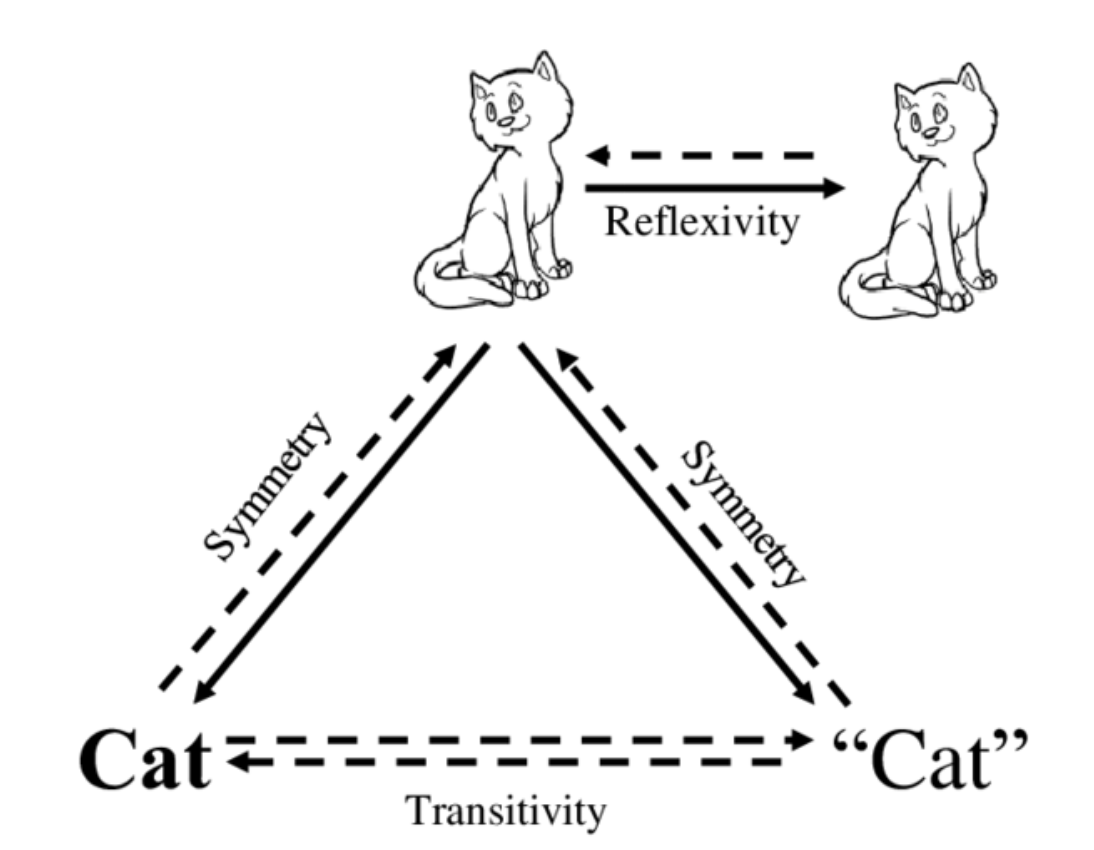
동치관계
𝑹 ∶ 집합 𝑨에서 관계
𝑹이 1)반사적, 2)대칭적, 3)추이적이면, 𝑹을 동치관계라고 부른다.
모듈로 합동
정수 m, n에 대해 양의 정수 d로 나머지 연산(mod)를 했을 때 같은 값이 나오는 경우.
ex) $8 \space mod\space5=3이고,
\space 13\space mod \space5 =3이므로 \space 8과 \space 13은 \space5에\space 관한 \space모듈로\space 합동이다.\
8 \equiv 13 \space(mod\space5)\space 이라고 \space표기한다.$
이러한 모듈로 합동은 반사적, 대칭적, 추이적인 성질을 가지므로 동치관계이다.(증명은 생략..)
동치류
𝑨 ∶ 집합, 𝑹 ∶ 𝑨에서의 동치관계일 때
𝑨의 임의의 원소 𝒂에 대해서 [𝒂] = { 𝒙 ∈ 𝑨 | (𝒂, 𝒙) ∈ 𝑹 를 𝒂의 동치류라고 부른다.
- 동치관계 임을 보임 ⇒ 동치류 찾기( [𝒂] = { 𝒙 ∈ 𝑨 | (𝒂, 𝒙) ∈ 𝑹)
'Computer Science > 이산수학' 카테고리의 다른 글
본 게시글은 대학 전공수업을 들으며 노션에 정리한 내용을 블로그로 옮긴 것으로, 노션 웹을 통해 최적화된 형태로 읽으시길 권장드립니다.특히 행렬 표현은 제대로 되지 않는 문제가 있습니다.(티스토리의 HTML 변환시 문제가 발생하는 것 같습니다.)(➡️ 노션 링크)
6강 - 관계
관계
미리 알아둘 사항

집합X에서 집합Y 로의 이항관계(binary relation) R은 𝑿 × 𝒀의 부분집합!
- (𝒙, 𝒚) ∈ 𝑹⇒ 𝒙𝑹𝒚로 표기
- ⇒ 𝒙는 𝒚와 𝑹의 관계가 있다.
- 𝑿 = 𝒀 이면 ⇒ 𝑹을 𝑿에서의 관계
- https://math24.net/binary-relations.html
- 예시

관계의 표현
화살표 도표
집합 A = {a,b,c,d,e}, 집합 B = {1,2,3,4,5,6} 이고
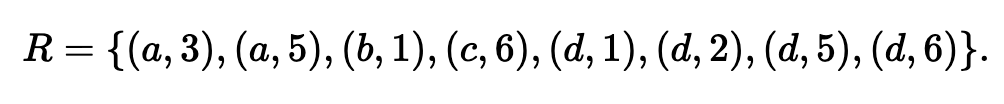
일때, 이를 화살표 도표로 나타내면

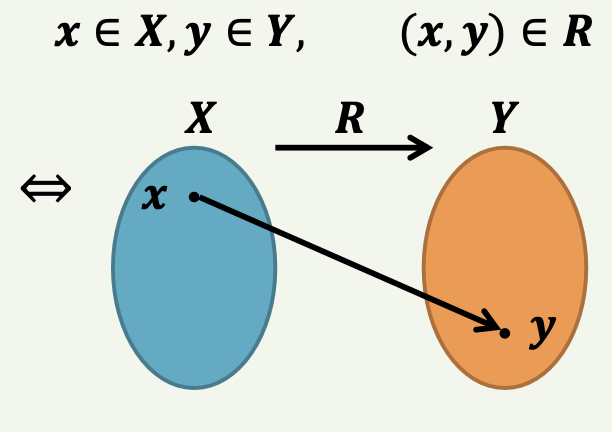
방향 그래프
그래프 *:** 점[꼭지점](vertex)과 선[변](edge)으로 이루어진 도형
- G = (V, E)
$$
A = {1, 2, 3, 4, 5} 이고, \
R = {(1,1), (1,2), (1,3), (3,3), (3,5), (4,1), (4,5), (5,4)}
$$
일 때의 방향그래프 :

https://math24.net/binary-relations.html
부울행렬
𝑨 = 𝟏, 𝟐, 𝟑
𝑻 = { (𝟏, 𝟏) , (𝟏, 𝟐) , (𝟐, 𝟏) , (𝟐, 𝟐) , (𝟑, 𝟏) , (𝟑, 𝟐) }
관계 T를 부울행렬로 나타내면
$M_T =\begin{pmatrix}
1 & 1 & 0 \
1 & 1 & 0 \
1 & 1 & 0 \
\end{pmatrix}
이고, \space |T| = 6$
관계의 성질
성질의 종류
반사적 (reflexive)
집합 A에서의 관계 R에 대해 ∀𝒂 ∈ 𝑨이면, (𝒂, 𝒂) ∈ 𝑹
즉, 모든 𝒂 ∈ 𝑨에 대해 (𝒂, 𝒂) ∈ 𝑹이면, R은 반사적이다.

https://math24.net/properties-relations.html
방향 그래프를 그렸을 때 자기 자신으로 돌아오는 게 모두 있는 것
대칭적 (symmetric)
∀𝒂, 𝒃 ∈ 𝑨, (𝒂, 𝒃) ∈ 𝑹 ⇒ (𝒃, 𝒂) ∈ 𝑹
모든 𝒂, 𝒃 ∈ 𝑨에 대해, (𝒂, 𝒃) ∈ 𝑹일 때 (𝒃, 𝒂) ∈ 𝑹이면 대칭적이다.

https://math24.net/properties-relations.html
가는게 있으면 오는게 있는 것
추이적 (transitive)
∀𝒂, 𝒃, 𝒄 ∈ 𝑨, ((𝒂, 𝒃) ∈ 𝑹 $\land$ (𝒃, 𝒄) ∈ 𝑹) ⇒ (𝒂, 𝒄) ∈ 𝑹
즉, 모든 𝒂, 𝒃, 𝒄 ∈ 𝑨에 대해, (𝒂, 𝒃) ∈ 𝑹이고 (𝒃, 𝒄) ∈ 𝑹일 때,
(𝒂, 𝒄) ∈ 𝑹이면 𝑹은 추이적이다.

https://math24.net/properties-relations.html
두번 돌아 가는 길이 있으면, 직접 가는 길도 있어야한다.
(노드 𝑎에서 𝑏로 가는 경로와 𝑏에서 𝑐로 가는 경로가 있다면,
𝑎에서 𝑐로 가는 경로도 존재한다.)
성질과 부울행렬
반사적
∀𝒂 ∈ 𝑨, (𝒂, 𝒂) ∈ 𝑹
$M_R = \begin{pmatrix}
1 & \cdots & \cdots \
\cdots & 1 & \cdots \
\cdots & \cdots & 1 \
\end{pmatrix}$
대칭적
∀𝒂, 𝒃 ∈ 𝑨, 𝒂, 𝒃 ∈ 𝑹 ⇒ (𝒃, 𝒂) ∈ 𝑹
$M_R = \begin{pmatrix}
1 & 1 & \cdots \
1 & 1 & \cdots \
\cdots & \cdots & 1 \
\end{pmatrix}$
추이적
∀𝒂, 𝒃, 𝒄 ∈ 𝑨, ((𝒂, 𝒃) ∈ 𝑹 ٿ (𝒃, 𝒄) ∈ 𝑹) ⇒ (𝒂, 𝒄) ∈ 𝑹
$M_R = \begin{pmatrix}
1 & 1 & 1 \
\cdots & 1 & 1 \
\cdots & \cdots & 1 \
\end{pmatrix}$
관계의 종류
역관계(Inverse Relation)
관계 𝑅이 𝐴에서 𝐵로의 관계라면, 역관계 𝑅−1는 𝐵에서 𝐴로의 관계.
𝑹−𝟏 = {(𝒚, 𝒙) | (𝒙, 𝒚) ∈ 𝑹 } ⊂ 𝒀 × 𝑿

https://math24.net/inverse-functions.html
합성관계(composition relation)
집합 𝑨, 𝑩, 𝑪, 𝑹을 𝑨에서 𝑩로의 관계, 𝑺를 𝑩에서 𝑪로의 관계라고 할 때
𝑹과 𝐒의 합성관계(composition relation)
𝑺 ∘ 𝑹 = {(𝒂, 𝒄) | 𝒂 ∈ 𝑨, 𝒃 ∈ 𝑩, 𝒄 ∈ 𝑪, (𝒂, 𝒃) ∈ 𝑹, (𝒃, 𝒄) ∈ 𝑺 }
𝑺 ∘ 𝑹 ⊂ 𝑨 × 𝑪 (𝑨에서 𝑪로의 관계)

https://math24.net/composition-relations
동치관계
𝑹 ∶ 집합 𝑨에서 관계
𝑹이 1)반사적, 2)대칭적, 3)추이적이면, 𝑹을 동치관계라고 부른다.

모듈로 합동
정수 m, n에 대해 양의 정수 d로 나머지 연산(mod)를 했을 때 같은 값이 나오는 경우.
ex) $8 \space mod\space5=3이고,
\space 13\space mod \space5 =3이므로 \space 8과 \space 13은 \space5에\space 관한 \space모듈로\space 합동이다.\
8 \equiv 13 \space(mod\space5)\space 이라고 \space표기한다.$
이러한 모듈로 합동은 반사적, 대칭적, 추이적인 성질을 가지므로 동치관계이다.(증명은 생략..)
동치류
𝑨 ∶ 집합, 𝑹 ∶ 𝑨에서의 동치관계일 때
𝑨의 임의의 원소 𝒂에 대해서 [𝒂] = { 𝒙 ∈ 𝑨 | (𝒂, 𝒙) ∈ 𝑹 를 𝒂의 동치류라고 부른다.
- 동치관계 임을 보임 ⇒ 동치류 찾기( [𝒂] = { 𝒙 ∈ 𝑨 | (𝒂, 𝒙) ∈ 𝑹)
